在光纤通信中，光线的传播依赖于纤芯和包层之间的折射率差异。

即，当光线从纤芯入射到界面上时，如果入射角大于临界角 θ0，将发生全反射，没有光能量透射至包层而泄漏出去，此即光纤导光原理。

反映到光纤的端面，在光纤端面的光线，当入射角必须小于光纤的孔径角 α0 ，此时才能在光纤中以全反射的方式传播。

这个孔径角，也就是咱们所说光纤的数值孔径 NA ：

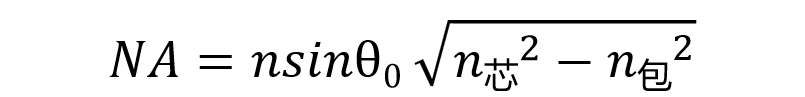
其中 n芯 表示纤芯的折射率， n包 表示包层的折射率。

也就是说，数值孔径光纤的折射率分布有关，反映了光纤接收光的能力的大小。对于阶跃型光纤和渐变型光纤，折射率分布如下图：

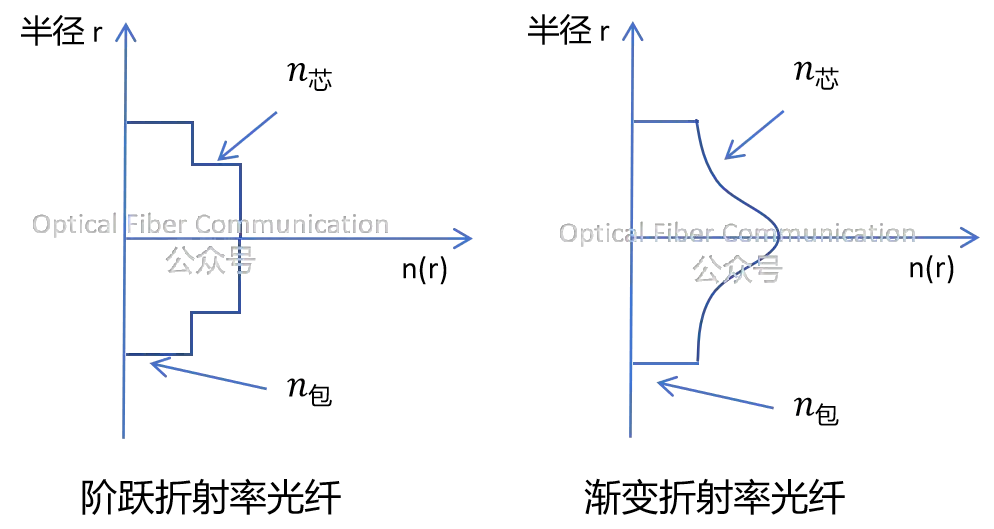
从上面的折射率分布图可以看出，阶跃折射率光纤，由于纤芯与包层的折射率可以看作是恒定的，因此各点数值孔径相同。而对于渐变型折射率的光纤，中心点数值孔径最大。

可能对于大多数朋友来说，认为只要光的入射小于孔径角的光就可以在光纤传输。除了NA，还要满足波导相长干涉的驻波条件。

啥是驻波条件？

在光纤中，驻波条件可以表述为：只有当光线在光纤的两个端面之间形成的光程差是光波长的整数倍时，光线才能在光纤中稳定传播。驻波公式我简化一下表示如下，原公式稍稍有些复杂。

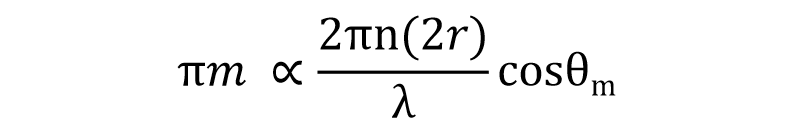
咱们只要知道只有一定入射角θ1、 θ2、θ3…θm的光线才能在波导内稳定传输即可。这些我们称之为光纤的模式，对就不同的模数 m 值。

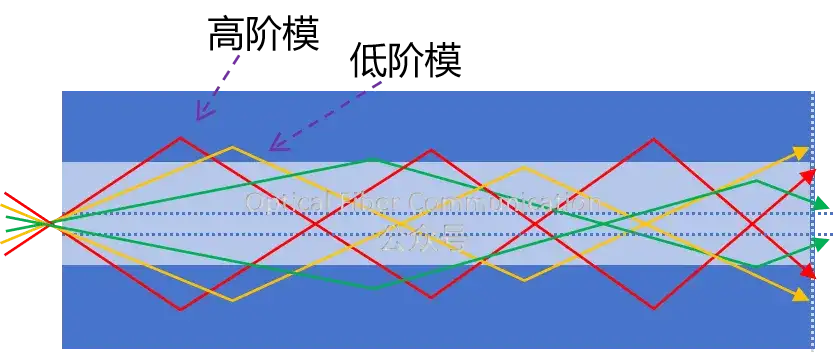
其中m越大，光进入包层越深，损耗越快，而且高阶模传输得慢，低阶模传输快。

从上面的讲解，我们已经知道，光纤中传输的光必须同时满足全反射条件和驻波条件。全反射与纤芯和包层折射率差有关，折射率差越大则孔径角越大。而驻波条件与纤芯尺寸有关，纤芯越大则允许的模式数量越多。

所以为了评估光纤能传输哪些模式，特别是我们需要何时才能保持光在光纤中以单模的方式传播。但是影响的因子太多，如光纤的物理尺寸、折射率差以及光波的频率，入射角等等。

为此，就弄了一个归一化频率 V值，只用这一个参数来描述光纤的结构特性就比较好办了。

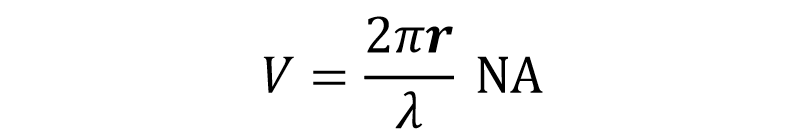
如果咱们的波长 λ 确定了，V 就取决于光纤的几何尺寸半径 r 和折射率的差异。V 越小，表示光纤限制光泄漏的能力越弱，允许传输的模式数量就越少。根据公式，增大波长 λ 或者包层的折射率，可以减小 V 值，从而使得传播的模式数量减小。所说根据贝塞尔函数并结合光纤模式理论得出了一个 V 值：2.405。这个值是光纤模式数量的分界线。如下图所示，表示了几种低阶线性偏振模与归一化频率 V 的示意关系。

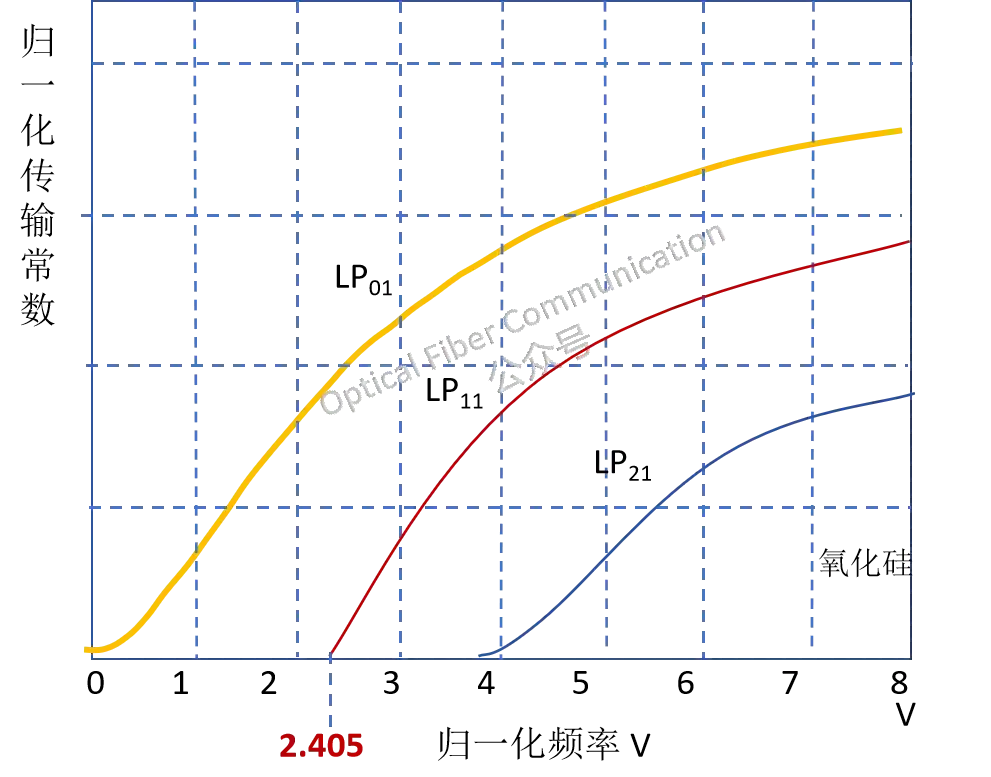
其中LP01为零次模，可以看出对于所有的 V 值都是存在的，是永远不会截止的模式，也称之为基模。LP11为1次模，在 V=2.405 时截止。因此，上面这种只允许基模LP01传输，即：

• 当 V < 2.405时，光纤中只有一个模式可以传播，成为单模光纤。
• 当 V > 2.405时，高阶模也将在光纤传输，例如 V 值在3~10之间的少模光纤。

与多模光纤相比，单模光纤的纤芯直径和纤芯与包层之间的折射率差要小得多。另外，从上面的公式中，我们还可以推导另外一个比较重要的公式，即截止波长：

当 λ < λ截止时则将不再满足单模条件，产生高阶模，导致传输损耗的增加，单模光纤就变成了多模光纤。因此，对于阶跃折射率光纤，可以利用 V 值来进行制定单模引导的条件。

不过，为了提升光纤的导光能力，并降低因弯曲造成的损耗，一般建议 V 值尽可能的设定在一个较高的水平。可以从上面的 V 值公式得出，增加纤芯的半径 r 或者纤芯的折射率都是可以使 V 变大的。

今天先到这里了，最后提一个小问题：如空芯光纤，光子带隙光纤等，是否存在2.405的 V 值，欢迎大家留言讨论！感谢阅读！